Hàm J(θ) cho Linear Regression

Dẫn nhập

Trong bài trước, chúng ta đã tìm hiểu về LINEAR REGRESSION VÀ HÀM hθ(x) CHO LINEAR REGRESSION.

Ở bài này Kteam sẽ giới thiệu đến các bạn Hàm J(θ) cho Linear Regression.

Nội dung

Để theo dõi bài này tốt nhất bạn cần có kiến thức về:

• LẬP TRÌNH PYTHON CƠ BẢN
• Xem qua bài GIỚI THIỆU MACHINE LEARNING VÀ CÀI ĐẶT NUMPY
• Xem qua bài MA TRẬN VÀ VECTOR VỚI NUMPY

Trong bài này chúng ta sẽ cùng tìm hiểu về:

• Hàm J(θ) là gì?
• Hàm J(θ) cho Linear Regression.
• Lập trình hàm J(θ) để tính độ chính xác với kết quả dự đoán có sẵn.
• Lưu ý về hàm J(θ).

Hàm J(θ) là gì ?

Qua bài trước Tèo đã có thể dự đoán được giá đất cho khách hàng, nhưng các vị khách hàng “thượng đế” của Tèo lại cho rằng giá đó là quá cao. Về phía Tèo, Tèo nghĩ giá mà Tèo dự đoán là giá chính xác nhất nhưng Tèo lại không biết được độ chính xác của mình. Vì thế, Tèo đã tìm hiểu về hàm J(θ) tìm ra độ chính xác của kết quả.

Với Machine Learning nói chung, chúng ta sẽ dùng kinh nghiệm E để thực hiện tác vụ T với độ chính xác P.

Hàm J(θ) có tác dụng “tính” độ chính xác P của tác vụ T nói chung, hay là hàm h_θ(x) nói riêng. Hàm h_θ(x) thực chất là hàm tính trung bình (một cách màu mè hơn) của tất cả những sai số khi dự đoán (kết quả dự đoán – kết quả thực tế).

Ví dụ:

Khi  ta có một hàm h_θ(x) chính xác:

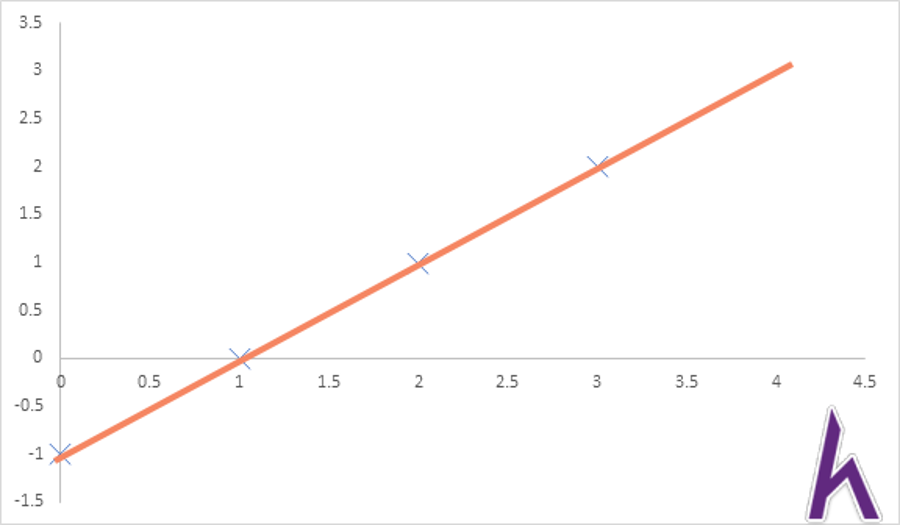
Thì hàm J(θ) sẽ bằng 0. Nhưng nếu hàm hθ(x) không chính xác:

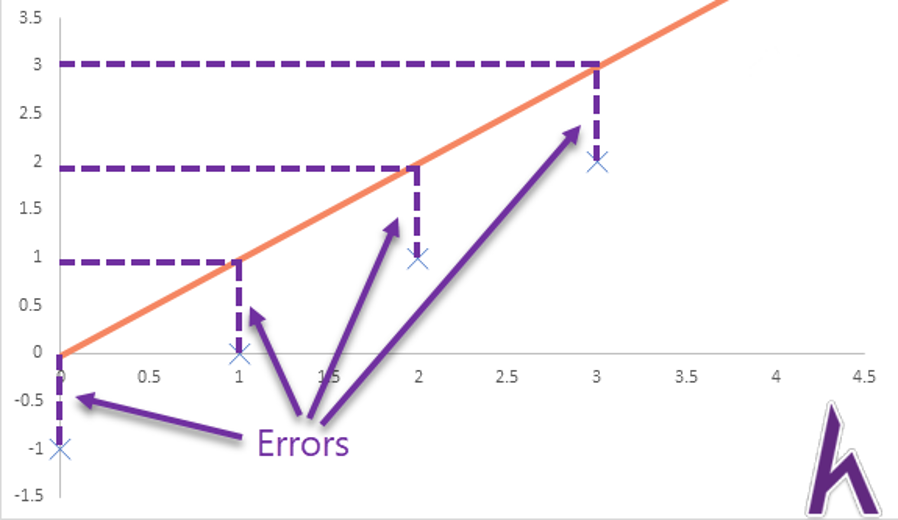
Thì J(θ) sẽ > 0. Trong trường hợp này là 0.5.

Hàm J(θ) cho Linear Regression.

Công thức

Phân tích

• Kí hiệu  là tổng của tất cả các training example (mẫu train). Bước này tương tự bước tính tổng trong việc tính trung bình.
•   là kết quả dự đoán dựa trên hàm h_θ(x).
•  là bình phương của sai số khi dự đoán. Vì thế hàm J(θ) còn có tên gọi khác là “hàm sai số bình phương”.
• Kết quả được chia 2   để thuận tiện cho việc sử dụng Gradient Descent  vì các phép tính tích phân sẽ triệt tiêu  (nếu bạn chưa học qua hoặc đã quên thì không sao! Kteam sẽ tính sẵn cho bạn trong các bài sau).

Ý nghĩa

Hàm J(θ) cho ta biết độ chính xác của hàm h_θ(x) hiện tại, giúp thuật toán tìm được hàm  h_θ(x) tối ưu nhất (trường hợp tốt nhất khi J(θ) = 0) để dự đoán được chính xác hơn.

Đồ thị

Đồ thị hàm J(θ) trong Linear Regression có dạng lõm (convex):

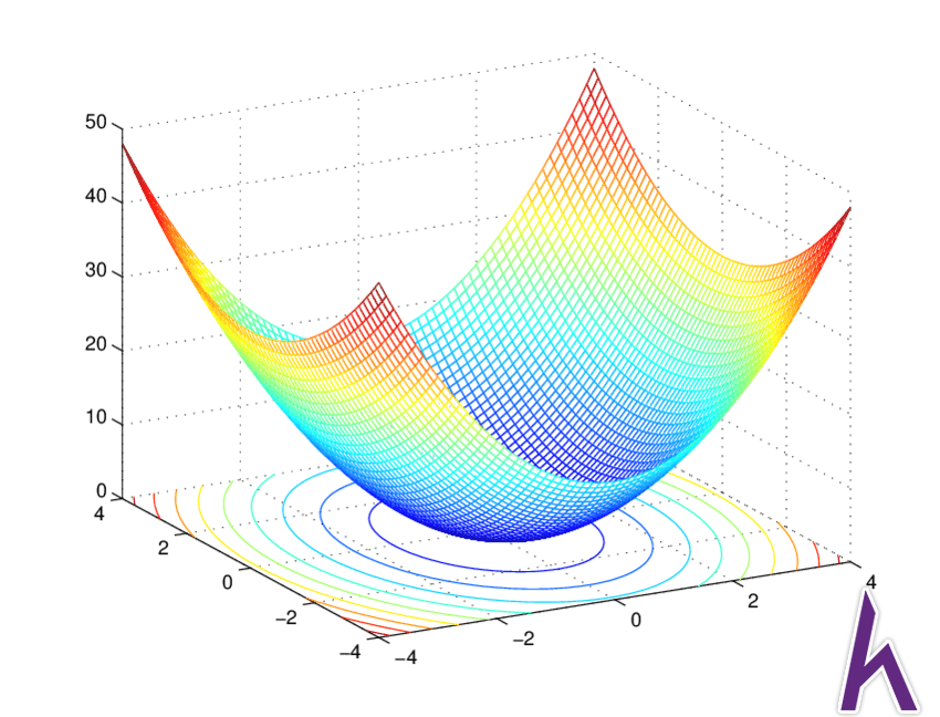
J(θ) “vectorized”

Hàm J(θ) “vectorized” có chức năng giống hoàn toàn hàm J(θ) thông thường, tốc độ cũng tương đồng nhưng không cần dùng hàm tổng ( ). Bạn có thể lựa chọn giữa 2 cách thiết kế hàm J(θ) tùy ý.

Lập trình hàm J(θ)

Load data

Kteam đã cung cấp sẵn resource của bài viết này tại:

Bài 4 - Resource

Trong file data có 3 cột, 2 cột đầu là X (các input), cột thứ 3 là y (kết quả).

Đầu tiên ta load raw data:

import numpy as np  
#import toàn bộ file data.txt
raw = np.loadtxt(data.txt', delimiter = ',')
1
2
3
4

Sau đó chia data vào ma trận X và vector y:

#tạo vector y = cột thứ 3 (index = 2)
y = raw[:,2]
#tạo ma trận X trống
X = np.zeros((np.size(y),np.size(raw,1)))
#thêm 1 vào cột đầu
X[:,0] = 1
#Thêm 2 cột sau vào
X[:,1:] = raw[:,0:2]
1
2
3
4
5
6
7
8

Predict function

Lúc này, Kteam khuyến khích bạn tạo 1 file .py mới để lưu những function để sau này có thể tái sử dụng.

Define lại hàm predict từ bài trước (hàm predict đơn giản chỉ là X * Theta, dùng để dự đoán kết quả):

#file: functions.py
def predict(X,Theta):
	return X @ Theta
1
2
3
4

Compute cost function

Bây giờ, chúng ta define hàm computeCost để tính J(θ). Parameter của hàm J(θ) sẽ gồm X,y và Theta.

#file: functions.py
import numpy as np
def computeCost(X,y,Theta):
	pass
1
2
3
4
5

Công thức của hàm J(θ) là , chúng ta sẽ lập trình từ trong ra ngoài. Đầu tiên là :

#file: functions.py
def computeCost(X,y,Theta):
	predicted = predict(X,Theta)
1
2
3
4

Sau đó tính :

#function computeCost
sqr_error = (predicted – y) ** 2
1
2
3

Tính tổng tất cả:

#function computeCost
sum_error = np.sum(sqr_error)
1
2
3

Nhân với  :

#function computeCost
m = np.size(y)
J = (1/(2*m))*sum_error
return J
1
2
3
4
5

Source code

#function computeCost
import numpy as np
def computeCost(X,y,Theta):
	sqr_error = (predicted – y)**2
	sum_error = np.sum(sqr_error)
	m = np.size(y)
	J = (1/(2*m))*sum_error
	return J
1
2
3
4
5
6
7
8
9

Compute cost vectorized function

Ở phiên bản vectorized, ta có thể viết hàm J(θ) đơn giản hơn:

#function computeCost_Vec
def computeCost_Vec(X,y,Theta):
	error = predict(X,Theta) – y
	m = np.size(y)
	J = (1/(2*m))*np.transpose(error)@error
	return J
1
2
3
4
5
6
7

Test hàm J(θ)

Để test hàm J(θ), ta tự tạo bộ Theta rồi thử hàm:

#file main.py
from functions import *
theta = np.array([1,2,3]) #bộ theta chính xác là [89597.909542,139.210674 ,-8738.019112]
print(computeCost(X,y,theta),computeCost_Vec(X,y,theta))
1
2
3
4
5

Nếu chính xác, với bộ theta [89597.909542,139.210674 ,-8738.019112] J(θ) sẽ là nhỏ nhất.

Source code

#file main.py
import numpy as np
from functions import *
#import toàn bộ file data.txt
raw = np.loadtxt('data.txt', delimiter = ',')
#tạo vector y = cột thứ 3 (index = 2)
y = raw[:,2]
#tạo ma trận X trống
X = np.zeros((np.size(y),np.size(raw,1)))
#thêm 1 vào cột đầu
X[:,0] = 1
#Thêm 2 cột sau vào
X[:,1:] = raw[:,0:2]

theta = np.array([1,2,3])
print(computeCost(X,y,theta),computeCost_Vec(X,y,theta))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Resources

Các bạn có thể download các file text được sử dụng trong bài viết tại:

Bài 4 - Resource

Kết luận

Qua bài này Kteam đã hướng dẫn các bạn về hàm J(θ) cho Linear Regression.

Ở bài sau, Kteam sẽ giới thiệu về PHƯƠNG PHÁP GRADIENT DESCENT CHO LINEAR REGRESSION – thuật toán giúp chúng ta tìm được parameter Theta phù hợp để hàm J(θ) nhỏ nhất.

Cảm ơn bạn đã theo dõi bài viết. Hãy để lại bình luận hoặc góp ý của mình để phát triển bài viết tốt hơn. Đừng quên “Luyện tập – Thử thách – Không ngại khó”.

---

Tải xuống

Tài liệu

Nhằm phục vụ mục đích học tập Offline của cộng đồng, Kteam hỗ trợ tính năng lưu trữ nội dung bài học Hàm J(θ) cho Linear Regression dưới dạng file PDF trong link bên dưới.

Ngoài ra, bạn cũng có thể tìm thấy các tài liệu được đóng góp từ cộng đồng ở mục TÀI LIỆU trên thư viện Howkteam.com

Đừng quên like và share để ủng hộ Kteam và tác giả nhé!

Thảo luận

Nếu bạn có bất kỳ khó khăn hay thắc mắc gì về khóa học, đừng ngần ngại đặt câu hỏi trong phần BÌNH LUẬN bên dưới hoặc trong mục HỎI & ĐÁP trên thư viện Howkteam.com để nhận được sự hỗ trợ từ cộng đồng.

CỘNG ĐỒNG HỎI ĐÁP HOWKTEAM.COM

GROUP THẢO LUẬN FACEBOOK